Estatística para todos: noções iniciais, curva normal (I)
Estatística para todos: noções iniciais, curva normal (II)
Estatística para todos: noções iniciais, curva normal (I)
Estatística para todos: noções iniciais, curva normal (II)
Exercícios da semana 2 - vídeoaulas 5 e 6
Videoaula 5
 Resolução:
Resolução:

Exercícios da semana 2 - vídeoaulas 7 e 8

b) A soma dos elementos da 31ª linha
Videoaula 8
1- A sequência (-10, -6, -2, 2, 6, 10, ...) é uma progressão aritmética de 1ª ordem porque a diferença entre um termo (a partir do 2º termo) e o anterior é constante. A sequência (3, 5, 9, 15, 23, ...) é uma progressão aritmética de 2ª ordem porque a diferença das diferenças (a partir do 2º termo) é constante. Determine uma fórmula posicional para a determinação do n-ésimo termo de cada uma dessas sequências.
Videoaula 5
1 - Determine a média, a moda e a mediana da seguinte distribuição de frequências:
 Resolução:
Resolução:
Videoaula 6
1 - Se a altura média de uma amostra, considerada normal, de pessoas é igual a 1,60 m e o desvio padrão das medidas das alturas é 0,20 m, qual é o porcentual da amostra contida entre 1,60 m e 1,80 m, isto é, no intervalo
P = 34,13%
Sequências, regularidades e séries (I)
Sequências, regularidades e séries (II)
Exercícios da semana 2 - vídeoaulas 7 e 8
Videoaula 7
- Para o exercício a seguir, serão úteis as seguintes fórmulas:
Termo geral de uma progressão aritmética → 
Soma de n termos de uma progressão aritmética → 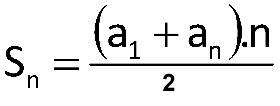
No triângulo
1
3 5
7 9 11
13 15 17 19
determine:
a) O primeiro elemento da 31ª linha.b) A soma dos elementos da 31ª linha
a)
an = n² – (n-1)
a31 = 31² – (31 -1)
a31 = 961 – 30
a31 = 931
b)
a31 = 1 + (31-1).2 = 991
Sn = (a1 + an) .n/2
S31 = (931 +991).31/2
S31 = 29791
Videoaula 8
1- A sequência (-10, -6, -2, 2, 6, 10, ...) é uma progressão aritmética de 1ª ordem porque a diferença entre um termo (a partir do 2º termo) e o anterior é constante. A sequência (3, 5, 9, 15, 23, ...) é uma progressão aritmética de 2ª ordem porque a diferença das diferenças (a partir do 2º termo) é constante. Determine uma fórmula posicional para a determinação do n-ésimo termo de cada uma dessas sequências.





